Solving ‘The Travelling Salesman Problem’ Through Quantum Computing

A classic algorithmic problem in the field of computer science known as the Traveling Salesman Problem (TSP) is a prime example of a combinatorial optimization problem.

What exactly is TSP? This mathematics classic involves finding the shortest possible route to visit N number of cities exactly once before returning to the origin city. However, as the number of cities increases, so do the possible routes and the computation time to find the optimal solution. While this problem can be solved using approximation methods, quantum computers could provide much better solutions and far more quickly at that. 

This is exactly what theoretical physicist Prof. Dr. Jens Eisert’s team demonstrated: that such problems can be solved better and faster with quantum computers.

Quantum computing utilizes hardware and algorithms that leverage quantum mechanics to solve complex problems beyond the reach of conventional, including supercomputers. Despite their power, supercomputers—massive classical computers with thousands of CPU and GPU cores—are limited by their reliance on 20th-century transistor technology when solving problems with a high degree of complexity. 

This is where quantum physics comes in. In contrast to classical computers, which encode information in binary bits (0s and 1s), quantum computers use quantum bits or qubits to run multidimensional quantum algorithms. 

Moreover, unlike conventional computers, which use fans for cooling, quantum computers require their quantum processors to be maintained at extremely cold temperatures to retain their quantum states. This is achieved through super-cooled superfluids. 

Superconductors are materials that exhibit a critical quantum mechanical effect, allowing electrons to move through them without resistance. As electrons pass through, they pair up to carry a charge across barriers. When two superconductors are placed on either side of an insulator, a Josephson junction is formed, which is used to conduct superconducting qubits.  

A qubit is useful in the important task of placing its quantum information into a state of superposition, a combination of qubit’s possible configurations. Groups of qubits in superposition are capable of creating complex, multidimensional computational spaces where complex problems can be represented.

Here, by the entanglement of two qubits, changes to one can impact the other directly, while when these entangled qubits are placed into a state of superposition, we get so many probabilities. Computation on a quantum computer works by preparing a superposition of all possible computational states, and through interference, solutions are found.

Of course, building a quantum computer with many qubits is a very complex procedure, though several methods are being explored as to what such computers can accomplish. 

According to Eisert, who leads a joint research group at Helmholtz-Zentrum Berlin (HZB), a research center for energy materials research, and the public research university Freie Universität Berlin:

“There are a lot of myths about it, and sometimes a certain amount of hot air and hype. However, we have approached the issue rigorously, using mathematical methods, and delivered solid results on the subject. Above all, we have clarified in what sense there can be any advantages at all.” 

The Critical Traveling Salesman Problem

An optimization problem, TSP is of great economic importance in the logistics and supply chain industry. It falls within the broader category of combinatorial optimization problems, which also includes job scheduling, resource allocation, portfolio optimization, and even protein folding, all critical to various sectors.

Given the social and economic significance of these problems, they have been the subject of intense research. As such, finding the answer to problems such as the most efficient supply chain and the cheapest delivery route has a positive impact on our daily lives.

However, optimizing the delivery routes for multiple destinations while considering various constraints such as traffic congestion, rising operational costs, sudden route changes, last-minute business appointments, and customer requests makes TSP even more challenging to solve. Despite these challenges, solving the TSP is crucial for the efficient delivery of goods, which ensures a viable business model. 

There are many benefits to solving this problem, including reducing the distance and hours traveled and saving fuel usage. Minimizing the distance traveled can help cut down the carbon footprint significantly, which translates to better air quality, slowed climate change, and economic growth. Moreover, solving the TSP can help with the on-time delivery of goods and timely meetings with clients, which enhances customer experience and field service businesses.

As we have seen, solving the problem not only helps businesses, but these benefits trickle down to the customers as well, enriching the experience for everyone involved.

Several methods can be used to solve the TSP problem. One such method is the ‘Brute-Force’ approach, which calculates all possible permutations to find the shortest route. In the branch-and-bound method, the problem is broken down into several series of subproblems, with each stage solution influencing the solution found at subsequent stages.

In dynamic programming, the focus is on avoiding redundant calculations. The Nearest Neighbor, meanwhile, is an approximation algorithm in which you begin with the starting location and then stop at the nearest one. Once all the cities are covered, you go back to the starting point. While practical and relatively quick, this method may not always provide an efficient route.

As technology advances, route planning and optimization can be done far more effectively. Artificial Intelligence (AI), in particular, can also help solve the problem by analyzing a massive amount of data quickly to help many modern enterprises make operational and strategic decisions.

Quantum computers are also being investigated to solve the problem; after all, they offer considerable computational speedups over classical computers. It has long been suggested that these computers may actually help improve approximations to these problems. 

Using Quantum Computing Techniques to Solve TSP

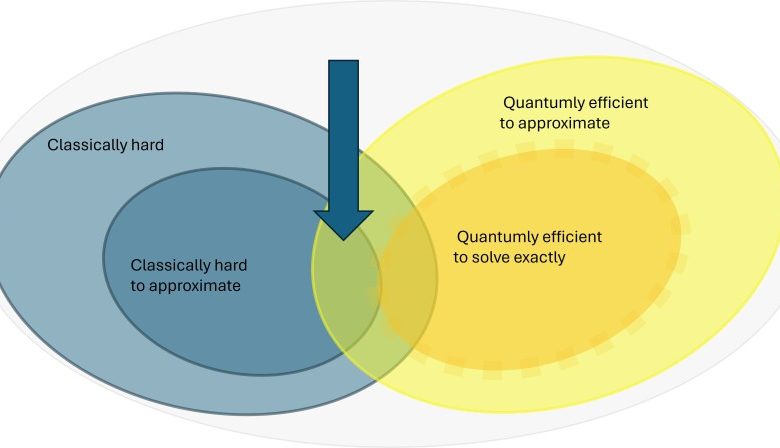
While quantum computing is garnering enormous interest and providing promising results for certain problems, the extent of this quantum advantage remains largely unexplored. 

As such, the study provided full constructive proof that quantum computers can actually outperform conventional computers for finding approximations to combinatorial optimization problems.

The latest study, led by Eisert and his colleague Jean-Pierre Seifert, used only analytical methods to evaluate just how a quantum computer with qubits can solve the problem of TSP. 

“We simply assume, regardless of the physical realization, that there are enough qubits and look at the possibilities of performing computing operations with them,” which reveals a resemblance to a common problem in cryptography, i.e., the encryption of data, explained Vincent Ulitzsch, a Ph.D. student at the Technical University of Berlin. 

Then, the team used the Shor algorithm, a quantum algorithm, to find the prime factors of an integer and solve a subclass of these optimization problems. With that, the computing time won’t explode any longer as the number of cities increases. It will only increase polynomially, i.e., with Nx, where x is a constant. This way, the solution obtained is also qualitatively much better than what is derived from the approximate solution using the conventional algorithm.

By using cryptographic concepts and computational learning theory, the study gives “fully constructive proof that quantum computers feature a super-polynomial advantage over classical computers in approximating combinatorial optimization problems.” 

The study further noted that the research team has made significant progress on the important question of what potential quantum computers may offer for approximating the solution of combinatorial optimization problems, which have substantial social and economic impacts.

The study was funded by the Einstein Research Unit, the Berlin Mathematics Research Center (MATH+ Cluster of Excellence), the BMBF (Hybrid), the BMWK (EniQmA), the Munich Quantum Valley, and the DFG. The Federal Ministry of Education and Research of Germany also provided financial support.

Exploring Quantum Computing’s Potential 

While a great achievement, this wasn’t the first time that quantum computing has been used to solve the traveling salesman problem. There have been many instances of enthusiasts and researchers looking into solving the problem by utilizing quantum computing. 

In December 2022, a paper proposed a quantum algorithm for the TSP based on the Grover Adaptive Search (GAS). Under the GAS framework, there are at least two fundamental difficulties—solutions may not be feasible, and the number of qubits of current quantum computers is very limited and cannot meet the minimum requirements, restricting the application of quantum algorithms for combinatorial optimization problems. 

As such, the paper polished the Hamiltonian Cycle Detection (HCD) oracle, which can remove impractical solutions automatically during the algorithm execution. They also designed an “anchor register” strategy to save qubit usage, fully considering the reversibility requirement of quantum computing and overcoming the difficulty of the used qubits not being simply overwritten or released. It allowed the study to require only 31 qubits, and the solution had a success rate of 86.71%.

In 2019, self-defined physics connoisseur Joseph Cammidge wrote about using an annealing quantum processor, which allowed him to solve the traveling salesman problem for seven cities and has the theoretical potential of solving for nine cities once technological limitations are eliminated. 

A new computing method, Quantum annealing, has shown the potential to solve optimization problems faster than classical techniques. Its theory implies that the qubits will achieve an optimal low-energy state when super-cooled. 

However, in 2021, a study funded by Supply Chain Digital & Data Science, Johnson & Johnson found the quantum annealer can only handle a problem size of 8 or fewer nodes, and its performance is subpar both in terms of time and accuracy compared to the classical solver.

The use of quantum computing to solve the TSP problem has been going on for a while now. Over two decades ago, in 2001, a study began searching for a quantum algorithm to solve the problem.

In the paper, Buckley Hopper of the University of Alabama looked at Grover’s and Shor’s quantum computer algorithms. He noted that Grover’s algorithm only provides a square root improvement, implying that it can’t make a classically intractable problem tractable on a quantum computer. As for Shor’s algorithm, Hopper observed that, while it can convert a presumably intractable prime factor problem into a tractable one on the quantum machine, it’s only suitable for a very specific type of problem. 

Overall, Hopper “did not find a satisfactory result for an algorithm for computing approximate solutions to the traveling salesman problem.”

A few years after that, the Institute of Electrical and Electronics Engineers (IEEE) presented a new algorithm for solving the problem, inspired by both genetic algorithms and quantum computing. The IEEE found that results from the application of the proposed algorithm on some instances of the Traveling Salesman Problem are considerably better than those provided by standard genetic algorithms.

Click here to learn about the current state of quantum computing.

Companies Working with Quantum Computing 

Now, let’s take a look at a couple of names that are working on the research and development of quantum computing:

#1. IBM

International Business Machines Corporation is engaged in a wide range of sectors, including AI, cloud services, IT, client financing, and commercial financing. The tech giant is also involved in quantum computing via its IBM Quantum Platform, which gives public and premium access to its cloud-based quantum computing services. These include a set of IBM’s prototype quantum processors, tutorials on quantum computation, and an interactive textbook.

Most recently, IBM scientists stated that they are another step closer to overcoming an obstacle that unlocks the game-changing potential of quantum computers. For this, they introduced a new quantum error-correcting code, which they say is about ten times more efficient than previous methods. 

Late last year, the company also launched the quantum computer called Condor, with 1,121 superconducting qubits that are arranged in a honeycomb pattern. IBM also unveiled IBM Quantum System Two, its first modular quantum computer and quantum-centric supercomputing architecture, which is scalable and hence can be upgraded with chips that will be launched in the next five years.

With a market cap of $175 billion, IBM’s shares are trading at $190.86, up 16.66% year-to-date (YTD). IBM has posted revenue (TTM) of $61.86 bln while having an EPS (TTM) of 8.03, P/E (TTM) of 23.76, and ROE (TTM) of 33.36%. The company pays a dividend yield of 3.48%.

#2. D-Wave Systems

This quantum computing company develops and delivers related systems, software, and services. Its products include The Leap and The Advantage, and it provides quantum applications for scheduling, logistics, drug discovery, manufacturing processes, and more. 

Earlier this month, D-Wave said quantum machines can now solve problems with real-world applications faster than any ordinary computer. Earlier this year, the company announced a quantum computer with 1,200 qubits, 10,000 couplers, and a 20x faster time-to-solution on hard optimization problems.

The company’s shares are currently trading at $1.86, up 138.6% year-to-date (YTD), with a market capitalization of $267 million. It reported $8.247 million in sales (TTM), -0.66 EPS (TTM), and -3.19 P/E (TTM), and announced over 20% growth in sales for both its Q4 and year-end 2023 results, while bookings increased by 34% and 89%, respectively. 

Interestingly, the company’s CEO, Dr. Alan Baratz, declared the firm’s momentum, citing the company’s multi-year strategic partnership with Zapata AI, the introduction of the 1,200+ qubit Advantage2 prototype, joint ventures with NEC Australia and Deloitte Canada, and the appointment of former Homeland Security Secretary Kirstjen Nielsen to the board of directors.

Conclusion

The market for quantum computing is expected to reach $6.5 billion in 2028, and its potential to solve the Traveling Salesman Problem (TSP) has ramifications for several industries, such as manufacturing, logistics, supply chain management, e-commerce, transportation, and research. After all, it can result in substantial benefits, notably boosting productivity, cutting expenses, and spurring innovation across diverse sectors.

Click here for the list of the best five quantum computing companies.